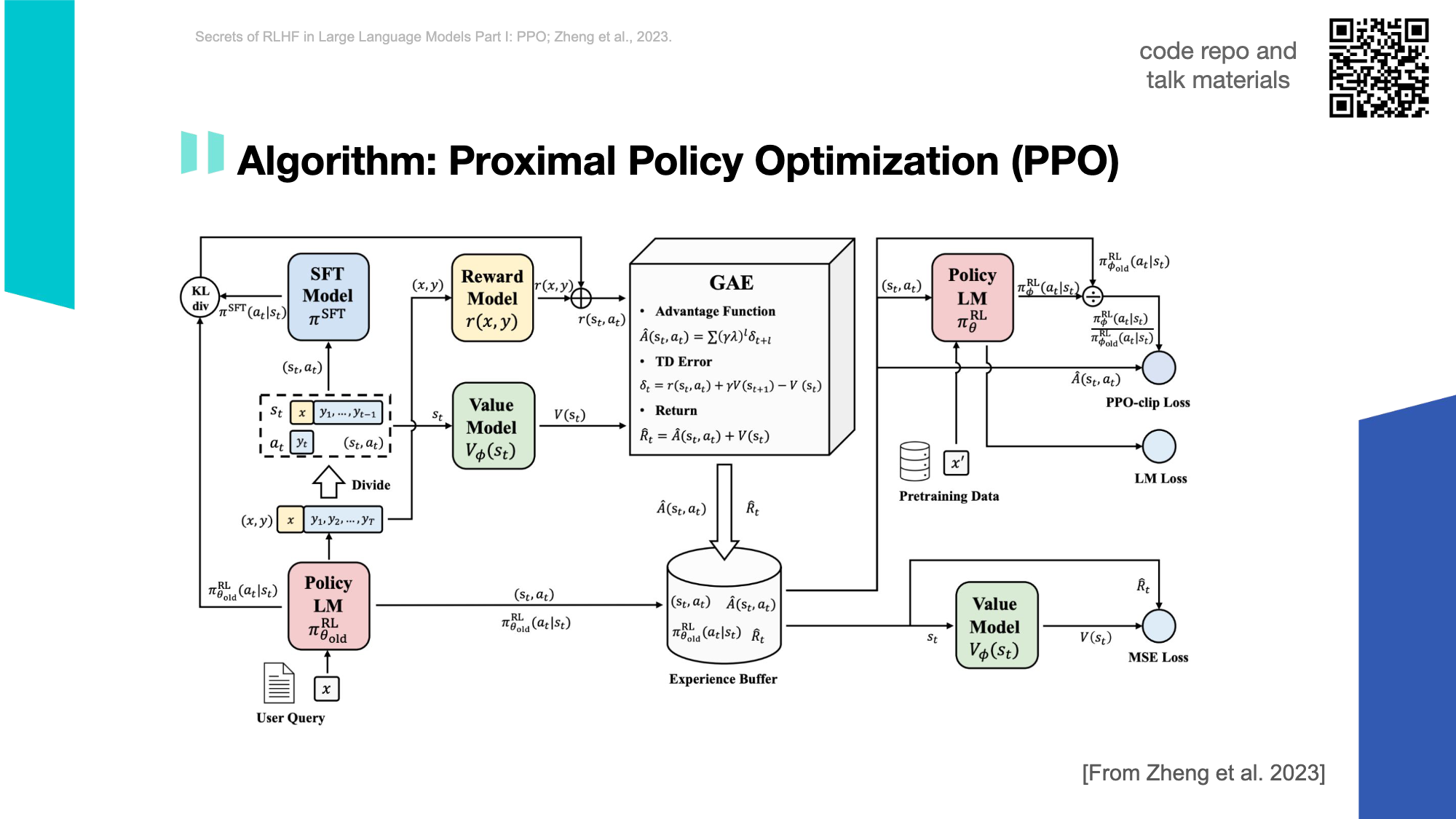
---

PPO算法

整体流程

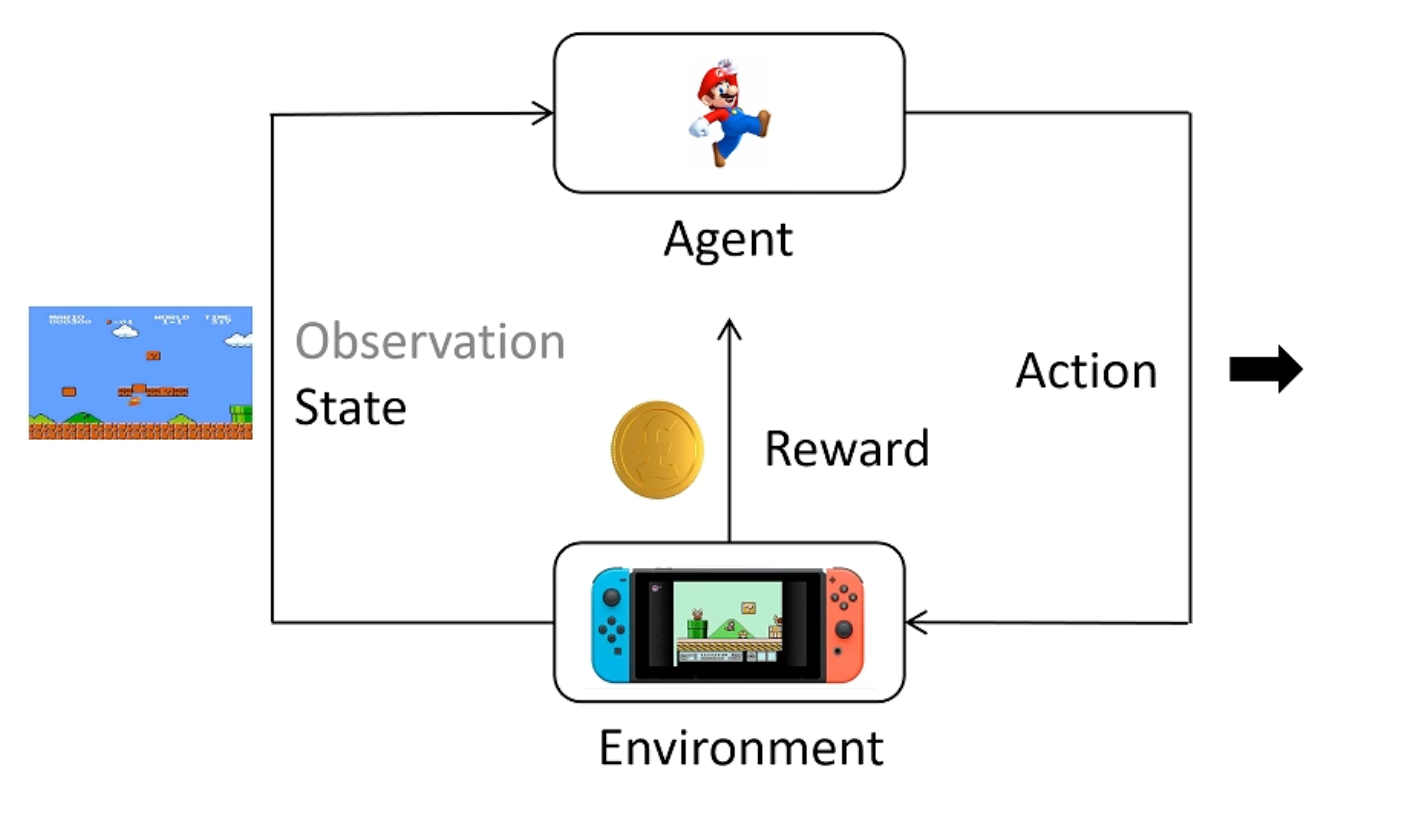
强化学习

一些基本概念

• action space：动作空间，即agent可以采取的动作的集合
• state space：状态空间，即agent可以观察到的状态的集合
• policy：策略，即agent在某个状态下采取某个动作的概率分布

\[\pi(a|s)\]

表示在状态$s$下，agent采取动作$a$的概率。这个策略一般是要学习的对象。

• trajectory：轨迹，即agent在环境中的一次交互序列

\[\tau = (s_0, a_0, s_1, a_1, \cdots)\]

其中$s_i$表示第$i$个状态，$a_i$表示第$i$个动作。

\[P(\tau) = P(s_0) \pi(a_0|s_0) P(s_1|s_0, a_0) \pi(a_1|s_1) \cdots\]

表示轨迹$\tau$的概率，其中$P(S_1

s_0, a_0)$表示在状态$s_0$下采取动作$a_0$后转移到状态$s_1$的概率，这种转移可以是确定性的，也可以是随机的。

• reward：奖励，即agent在某个状态下采取某个动作后得到的奖励

\[r(s, a)\]

表示在状态$s$下，agent采取动作$a$后得到的奖励。

• return：回报，对于一个轨迹$\tau$，其回报定义为

\[R(\tau) = \sum_{t=0}^{\infty} r(s_t, a_t)\]

即轨迹中所有奖励的和。

强化学习的目标

强化学习的目标是找到一个策略$\pi$，使得agent在环境中的return最大。这个return最大可以用两种方式来定义：

对于任意的状态$s$，$\pi$给出相应的动作$a$，使得agent的 期望 回报最大

对于$\pi$生成的所有轨迹$\tau$，使得所有轨迹的 期望 回报最大

假设$\theta$是策略$\pi$的参数，那么期望回报可以表示为

\[\begin{aligned} &E(R(\tau))_{\tau \sim P_{\theta}(\tau)}\\ =& \sum_{\tau} P_{\theta}(\tau) R(\tau)\\ \end{aligned}\]

对他求导，可以得到 \(\begin{aligned} &\nabla_{\theta} \sum_{\tau} P_{\theta}(\tau) R(\tau) \\ =& \sum_{\tau} R(\tau) \nabla_{\theta} P_{\theta}(\tau)\\ =& \sum_{\tau} R(\tau) P_{\theta}(\tau) \frac{\nabla_{\theta} P_{\theta}(\tau)}{P_{\theta}(\tau)}\\ \approx& \frac{1}{N} \sum_{i=1}^{N} R(\tau_i) \frac{\nabla_{\theta} P_{\theta}(\tau_i)}{P_{\theta}(\tau_i)} \quad // \text{采样N个轨迹，用这N个轨迹的平均值来估计期望} \\ =& \frac{1}{N} \sum_{i=1}^{N} R(\tau_i) \nabla_{\theta} \log P_{\theta}(\tau_i) \quad // \text{由于$\nabla_{\theta} \log P_{\theta}(\tau_i) = \frac{\nabla_{\theta} P_{\theta}(\tau_i)}{P_{\theta}(\tau_i)}$} \\ =& \frac{1}{N} \sum_{i=1}^{N} R(\tau_i) \nabla_{\theta} \log\prod_{t=0}^{T} P_{\theta}(a_t|s_t)P(s_{t+1}|s_t, a_t) \quad // \text{轨迹$\tau_i$的概率$P_{\theta}(\tau_i)$可以展开} \\ =& \frac{1}{N} \sum_{i=1}^{N} R(\tau_i) \nabla_{\theta} \log\prod_{t=0}^{T} P_{\theta}(a_t|s_t) \quad // \text{$P(s_{t+1}|s_t, a_t)$是环境的转移概率，与策略无关} \\ =& \frac{1}{N} \sum_{i=1}^{N} R(\tau_i) \sum_{t=0}^{T} \nabla_{\theta} \log P_{\theta}(a_t|s_t) \quad // \text{对数代入} \\ \end{aligned}\)

如此，我们就得到了一个可以用来更新策略参数$\theta$的梯度。

接下来，我们可以定义loss function为

\[Loss = -\frac{1}{N} \sum_{i=1}^{N} R(\tau_i) \sum_{t=0}^{T} \log P_{\theta}(a_t|s_t)\]

Action Value Function：$Q_\theta(s, a)$，表示在状态$s$下采取动作$a$后的回报期望。

\[Q_\theta(s, a) = E[R_\theta(s, a)]\]

State Value Function：$V_\theta(s)$，表示在状态$s$下的回报期望。

\[V_\theta(s) = E[R_\theta(s)] = \sum_{a} \pi_\theta(a|s) Q_\theta(s, a)\]

Advantage Function：$A_\theta(s_t, a_t)$，表示在状态$s_t$下采取动作$a_t$相对于在状态$s_t$下采取动作$a$的优势。

使用Advantage Function来替换上面的$R(\tau)$，我们可以得到：

\[\begin{aligned} &\sum_{i=1}^{N} \sum_{t=0}^{T_{i}} A_{\theta}(s_{t, i}, a_{t, i}) \nabla_{\theta} \log P_{\theta}(a_{t, i}|s_{t, i}) \\ \end{aligned}\]

优势函数的计算

接下来，我们只要关注如何计算Advantage Function即可。

\[A_\theta(s_t, a_t) = Q_\theta(s_t, a_t) - V_\theta(s_t) = r(s_t, a_t) + \gamma V_\theta(s_{t+1}) - V_\theta(s_t)\]

其中$\gamma$是折扣因子，当设置为1的时候，表示不折扣，即为前面推导的结果。 但在实际应用中，我们一般会设置一个小于1的值，表示未来的奖励不如当前的奖励重要。

同样的，我们可以推导

\[\begin{aligned} V_{\theta} (s_t) & = \overbrace{\left(\sum_{a} \pi_{\theta}(a|s_t) r(s_t, a)\right)}^{做一次采样} &+ \gamma V_{\theta}(s_{t+1}) \\ & = r(s_t, a_t) &+ \gamma V_{\theta}(s_{t+1}) \\ &= r_t + \gamma V_{\theta}(s_{t+1}) \quad \end{aligned}\]

我们用$r_t$简化$r(s_t, a_t)$，表示在状态$s_t$下采取动作$a_t$后得到的奖励。

这时候，其实我们可以得到advantage function的另一种计算方式：

\[\begin{aligned} A_{\theta}^1(s_t, a_t) & = r_t + \gamma V_{\theta}(s_{t+1}) - V_{\theta}(s_t) \\ A_{\theta}^2(s_t, a_t) & = r_t + \gamma r_{t+1} + \gamma^2 V_{\theta}(s_{t+2}) - V_{\theta}(s_t)\\ &= A_{\theta}^1(s_t, a_t) + \gamma A_{\theta}^1(s_{t+1}, a_{t+1}) \quad // \text{我们用$A_{\theta}^1$来计算$A_{\theta}^2$} \\ &= A_{\theta,t} + \gamma A_{\theta,t+1} \quad // \text{我们用$A_{\theta,t}$来简化$A_{\theta}^1$} \\ \cdots \\ A_{\theta}^T(s_t, a_t) & = \left(\sum_{i=0}^{T-1} \gamma^i r_{t+i}\right) + \gamma^T V_{\theta}(s_{t+T}) - V_{\theta}(s_t) \\ &= \sum_{i=0}^{T-1} \gamma^i A_{\theta,t+i} \end{aligned}\]

从$A_{\theta}^1$到$A_{\theta}^T$，偏差（bias）越来越小，但是方差（variance）越来越大。

广义优势估计（GAE, Generalized Advantage Estimation）

那肯定要trade-off了，我们可以用一个参数$\lambda$来控制这个trade-off。

\[\begin{aligned} A_{\theta}^{GAE}(s_t, a_t) &= (1-\lambda) \sum_{l=0}^{T} \lambda^l A_{\theta}^l(s_t, a_t)\\ &= (1-\lambda) \sum_{l=0}^{T} \lambda^l \left(\sum_{i=0}^{T-l} \gamma^i A_{\theta,t+i}\right)\\ &= \sum_{l=0}^{T} (\lambda\gamma)^l A_{\theta,t+l} \end{aligned}\]

回到梯度的计算，我们可以得到

\[\begin{aligned} \sum_{i=1}^{N} \sum_{t=0}^{T_{i}} A_{\theta}^{GAE}(s_{t, i}, a_{t, i}) \nabla_{\theta} \log P_{\theta}(a_{t, i}|s_{t, i}) \\ \end{aligned}\]

所以，在模型输出中，除了得到$\pi$的输出，还要得到$V$的输出。

从on-policy到off-policy

重要性采样（Importance Sampling）

假设我们有两个策略$\pi$和$\pi’$，我们可以用$\pi$生成的轨迹来估计$\pi’$的期望回报。其中，$\pi$是参考策略，$\pi’$是目标策略。

\[\begin{aligned} &E_{\pi'}[R(\tau)] \\ =& \sum_{\tau} P_{\pi'}(\tau) R(\tau) \\ =& \sum_{\tau} P_{\pi'}(\tau) \frac{P_{\pi}(\tau)}{P_{\pi}(\tau)} R(\tau) \\ =& \sum_{\tau} P_{\pi'}(\tau) \frac{P_{\pi}(\tau)}{P_{\pi}(\tau)} R(\tau) \\ =& \sum_{\tau} P_{\pi}(\tau) \frac{P_{\pi'}(\tau)}{P_{\pi}(\tau)} R(\tau) \\ =& E_{\pi}[R(\tau) \frac{P_{\pi'}(\tau)}{P_{\pi}(\tau)}] \end{aligned}\]

这里，$\frac{P_{\pi’}(\tau)}{P_{\pi}(\tau)}$就是重要性采样比率。

梯度公式的推导也是类似的。

\[\begin{aligned} &\sum_{i=1}^{N} \sum_{t=0}^{T_{i}} A_{\theta'}(s_{t, i}, a_{t, i})^{GAE} \nabla_{\theta'} \log P_{\theta'}(a_{t, i}|s_{t, i}) \\ =& \sum_{i=1}^{N} \sum_{t=0}^{T_{i}} A_{\theta}^{GAE}(s_{t, i}, a_{t, i}) \frac{P_{\theta'}(a_{t, i}|s_{t, i})}{P_{\theta}(a_{t, i}|s_{t, i})} \nabla_{\theta'} \log P_{\theta'}(a_{t, i}|s_{t, i}) \\ =& \sum_{i=1}^{N} \sum_{t=0}^{T_{i}} A_{\theta}^{GAE}(s_{t, i}, a_{t, i}) \frac{P_{\theta'}(a_{t, i}|s_{t, i})}{P_{\theta}(a_{t, i}|s_{t, i})} \frac{\nabla_{\theta'} P_{\theta'}(a_{t, i}|s_{t, i})}{P_{\theta'}(a_{t, i}|s_{t, i})} \\ =& \sum_{i=1}^{N} \sum_{t=0}^{T_{i}} A_{\theta}^{GAE}(s_{t, i}, a_{t, i}) \frac{\nabla_{\theta'} P_{\theta'}(a_{t, i}|s_{t, i})}{P_{\theta}(a_{t, i}|s_{t, i})} \\ \end{aligned}\]

即，我们可以用$\pi$生成的轨迹来估计$\pi’$的梯度，换句话说，我们可以用$\pi$的advantage function来估计$\pi’$的advantage function。

对应的loss function为

\[Loss_{\text{importance sampling}} = -\frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T_{i}} A_{\theta}^{GAE}(s_{t, i}, a_{t, i}) \frac{P_{\theta'}(a_{t, i}|s_{t, i})}{P_{\theta}(a_{t, i}|s_{t, i})}\]

稳定性

当目标策略和参考策略相差较大时，重要性采样的方差会变得很大，研究者采用了两种方法:

• clip: 对于

\[\frac{P_{\theta'}(a_{t, i}|s_{t, i})}{P_{\theta}(a_{t, i}|s_{t, i})}\]

进行截断，使其不超过一个阈值，超过阈值的部分直接截断，即不参与梯度的计算。

• KL divergence: 通过控制两个策略之间的KL散度，使得两个策略之间的差距不会太大。

KL 散度的定义为

\[KL(P_{\theta'}||P_{\theta}) = E_{P_{\theta'}}[\log \frac{P_{\theta'}(\cdot)}{P_{\theta}(\cdot)}] = \sum_{x} P_{\theta'}(x) \log \frac{P_{\theta'}(x)}{P_{\theta}(x)}\] \[Loss_{\text{KL}} = -\frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T_{i}} A_{\theta}^{GAE}(s_{t, i}, a_{t, i}) \nabla_{\theta'} \log P_{\theta'}(a_{t, i}|s_{t, i}) + \beta KL(P_{\theta'}(\cdot|s_{t, i})||P_{\theta}(\cdot|s_{t, i}))\]